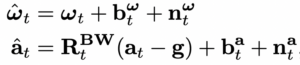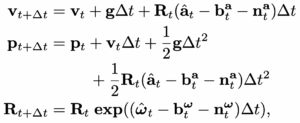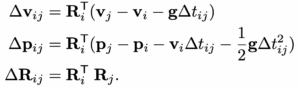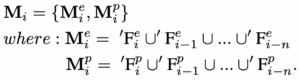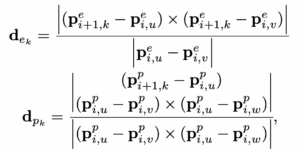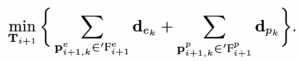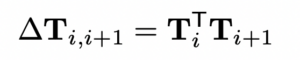本文对LIO-SAM:Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping论文进行研读。

论文：https://github.com/TixiaoShan/LIO-SAM/blob/master/config/doc/paper.pdf

代码：TixiaoShan/LIO-SAM

一、摘要 Abstract

We propose a framework for tightly-coupled lidar inertial odometry via smoothing and mapping, LIO-SAM, that achieves highly accurate, real-time mobile robot trajectory es- timation and map-building. LIO-SAM formulates lidar-inertial odometry atop a factor graph, allowing a multitude of relative and absolute measurements, including loop closures, to be incorporated from different sources as factors into the system. The estimated motion from inertial measurement unit (IMU) pre-integration de-skews point clouds and produces an initial guess for lidar odometry optimization. The obtained lidar odometry solution is used to estimate the bias of the IMU. To ensure high performance in real-time, we marginalize old lidar scans for pose optimization, rather than matching lidar scans to a global map. Scan-matching at a local scale instead of a global scale significantly improves the real-time performance of the system, as does the selective introduction of keyframes, and an efficient sliding window approach that registers a new keyframe to a fixed-size set of prior “sub-keyframes.” The proposed method is extensively evaluated on datasets gathered from three platforms over various scales and environments.

本论文提出一种紧耦合的平滑建图激光惯导里程计框架，LIO-SAM，完成高准确度、实时的移动机器人轨迹估计和地图构建。LIO-SAM在因子图上制定了一个激光惯导里程计，允许许多相对和绝对测量，包括闭环，从不同的来源作为因子图的输入纳入系统中。IMU预积分的运动估计对点云进行去畸变并产生激光里程计优化的初始估计。激光雷达里程计方案用于估计IMU的零偏。为了确保在实时环境下得到较好的性能，在姿态优化的时候边缘化掉旧的激光雷达帧，而不是将激光雷达点云帧匹配到全局地图中。局部尺度而不是全局尺度上的扫描匹配可以显著高系统的实时性能，选择性引入关键帧以及有效的滑动窗口方法，将新的关键帧注册到固定大小的“子关键帧”中。提出的方法，在不同尺度和环境下，从三个平台搜集的数据集上，进行了广泛的评估。

二、引言 Introduction

State estimation, localization and mapping are fundamental prerequisites for a successful intelligent mobile robot, required for feedback control, obstacle avoidance, and planning, among many other capabilities. Using vision-based and lidar-based sensing, great efforts have been devoted to achieving high-performance real-time simultaneous lo- calization and mapping (SLAM) that can support a mobile robot’s six degree-of-freedom state estimation. Vision-based methods typically use a monocular or stereo camera and triangulate features across successive images to determine the camera motion. Although vision-based methods are especially suitable for place recognition, their sensitivity to initialization, illumination, and range make them unreliable when they alone are used to support an autonomous navigation system. On the other hand, lidar-based methods are largely invariant to illumination change. Especially with the recent availability of long-range, high-resolution 3D lidar, such as the Velodyne VLS-128 and Ouster OS1-128, lidar becomes more suitable to directly capture the fine details of an environment in 3D space. Therefore, this paper focuses on lidar-based state estimation and mapping methods.

状态估计、定位与建图是一个成功的智能移动机器人的基础前提，这是反馈控制、避障和规划等许多其他功能所必需的。利用基于视觉和基于激光雷达的感知，人们已经付出了巨大的努力致力于实现移动机器人的高性能实时同步定位与建图，它可以支持移动的六自由度的状态估计。基于视觉的方法通常采用单目或者深度相机，并通过连续图像的三角化特征来确定相机运动。尽管基于视觉的方法特别适合位置识别，但是视觉方法对初始化、光照、距离的敏感性，使得它们在单独用于支持自动导航系统时不是很可靠。另一方面，基于激光雷达的方法在很大程度上不受光照变化的影响。特别是随着最近提出的远距离、高分辨率三维激光雷达，比如Velodyne128线以及Ouster128线，激光雷达变得更适合直接捕捉三维空间环境中的细节。因此，本文着重研究基于激光雷达的状态估计和建图方法。

Many lidar-based state estimation and mapping methods have been proposed in the last two decades. Among them, the lidar odometry and mapping (LOAM) method proposed in [1] for low-drift and real-time state estimation and mapping is among the most widely used. LOAM, which uses a lidar and an inertial measurement unit (IMU), achieves state-of- the-art performance and has been ranked as the top lidar- based method since its release on the KITTI odometry benchmark site [2]. Despite its success, LOAM presents some limitations – by saving its data in a global voxel map, it is often difficult to perform loop closure detection and incorporate other absolute measurements, e.g., GPS, for pose correction. Its online optimization process becomes less efficient when this voxel map becomes dense in a feature-rich environment. LOAM also suffers from drift in large-scale tests, as it is a scan-matching based method at its core.

最近二十年，出现了许多基于激光雷达的状态估计和建图方法。其中，LOAM方法，在低偏移和实时状态估计和建图中，是应用最广泛的。LOAM采用激光雷达和IMU达到了最好的性能，并自从KITTI里程计Benchmark榜单发布以来一直被列为最好的激光雷达方法。尽管LOAM取得了成功，但还是存在一些限制：通过将数据保存在全局体素地图中，通常很难执行回环检测以及结合其他，比如GPS，绝对测量值用于姿态校正。当体素地图在特征丰富的环境中变得稠密时，LOAM的在线优化过程就会变得效率很低。LOAM在大规模测试中也存在漂移问题，因为它的核心是一种基于scan-match扫描匹配的方法。

In this paper, we propose a framework for tightly-coupled lidar inertial odometry via smoothing and mapping, LIO- SAM, to address the aforementioned problems. We assume a nonlinear motion model for point cloud de-skew, estimating the sensor motion during a lidar scan using raw IMU measurements. In addition to de-skewing point clouds, the estimated motion serves as an initial guess for lidar odometry optimization. The obtained lidar odometry solution is then used to estimate the bias of the IMU in the factor graph. By introducing a global factor graph for robot trajectory estimation, we can efficiently perform sensor fusion using lidar and IMU measurements, incorporate place recognition among robot poses, and introduce absolute measurements, such as GPS positioning and compass heading, when they are available. This collection of factors from various sources is used for joint optimization of the graph. Additionally, we marginalize old lidar scans for pose optimization, rather than matching scans to a global map like LOAM. Scan-matching at a local scale instead of a global scale significantly im- proves the real-time performance of the system, as does the selective introduction of keyframes, and an efficient sliding window approach that registers a new keyframe to a fixed- size set of prior “sub-keyframes.”

本文中，提出一个通过平滑和建图的紧耦合激光惯导里程计框架，LIO-SAM，用来解决上面提到的问题。我们假设一个点云去畸变后的非线性运动模型，使用原始IMU测量数据估计激光雷达扫描过程中的传感器运动。除了点云去畸变，运动估计作为激光雷达里程计优化的初始估计。得到的激光雷达里程计解决方案用于估计因子图中IMU零偏。通过引入机器人轨迹估计的全局因子图，我们利用激光雷达和IMU测量有效地进行传感器融合，结合机器人姿态之间的位置识别，并在可用的时候，引入GPS定位或者指南针航向等绝对测量。不同来源因子的集合用于因子图的联合优化。此外，我们边缘化旧的激光雷达扫描来优化姿态，而不是类似LOAM那样将扫描匹配到全局地图中。局部尺度而不是全局尺度上的扫描匹配scan-match可以显著提高系统的实时性能，以及选择性地引入关键帧和一种有效的滑动窗口方法，将新的关键帧注册到之前的“子关键帧”集合中。

The main contributions of our work can be summarized as follows:

• A tightly-coupled lidar inertial odometry framework built atop a factor graph, that is suitable for multi-sensor fusion and global optimization.
• An efficient, local sliding window-based scan-matching approach that enables real-time performance by regis- tering selectively chosen new keyframes to a fixed-size set of prior sub-keyframes.
• The proposed framework is extensively validated with tests across various scales, vehicles, and environments.

本文工作的主要贡献总结如下：

• 在因子图上建立一个紧耦合的激光惯导里程计框架，适用于多传感器融合和全局优化。
• 提出一种高效的，基于局部滑动窗口的扫描匹配方法，通过有选择性地挑选新关键帧注册到固定大小的先前的子关键帧集合上，来达到实时的性能。
• 提出的框架在不同尺度、车辆以及环境中的测试得到了广泛的验证。

三、相关工作 Related Work

Lidar odometry is typically performed by finding the relative transformation between two consecutive frames us- ing scan-matching methods such as ICP [3] and GICP [4]. Instead of matching a full point cloud, feature-based matching methods have become a popular alternative due to their computational efficiency. For example, in [5], a plane- based registration approach is proposed for real-time lidar odometry. Assuming operations in a structured environment, it extracts planes from the point clouds and matches them by solving a least-squares problem. A collar line-based method is proposed in [6] for odometry estimation. In this method, line segments are randomly generated from the original point cloud and used later for registration. However, a scan’s point cloud is often skewed because of the rotation mechanism of modern 3D lidar, and sensor motion. Solely using lidar for pose estimation is not ideal since registration using skewed point clouds or features will eventually cause large drift.

激光雷达里程计通常是通过ICP【3】或者GICP【4】等scan-match扫描匹配算法查找两个连续帧之间的相对转换来进行的。除了匹配一整片点云，基于特征的匹配方法已经成为一种流行的替代方法。例如，文献【5】中提出的基于平面的实时激光雷达匹配方法。假设在结构化环境中进行操作，它从点云中提取平面，并通过解决最小二乘问题对它们进行匹配。文献【6】中提出一种基于项圈线的里程计估计方法。在该方法中，从原始点云中随机生成线段，并用于之后的点云配准。然而，由于现代三维激光雷达的旋转机制和传感器的运动，扫描的点云通常都是倾斜的。仅仅使用激光雷达进行姿态估计并不是理想的，因为使用点云或特征进行配准最终会导致大的漂移。

Therefore, lidar is typically used in conjunction with other sensors, such as IMU and GPS, for state estimation and mapping. Such a design scheme, utilizing sensor fusion, can typically be grouped into two categories: loosely-coupled fusion and tightly-coupled fusion. In LOAM [1], IMU is introduced to de-skew the lidar scan and give a motion prior for scan-matching. However, the IMU is not involved in the optimization process of the algorithm. Thus LOAM can be classified as a loosely-coupled method. A lightweight and ground-optimized lidar odometry and mapping (LeGO-LOAM) method is proposed in [7] for ground vehicle map- ping tasks [8]. Its fusion of IMU measurements is the same as LOAM. A more popular approach for loosely-coupled fusion is using extended Kalman filters (EKF). For example, [9]- [13] integrate measurements from lidar, IMU, and optionally GPS using an EKF in the optimization stage for robot state estimation.

因此，激光雷达通常与其他传感器联合使用，比如IMU或者GPS，用于姿态估计以及建图。这种利用传感器融合的设计方案，通常可以分为两类：松耦合融合以及紧耦合融合。在LOAM中，引入IMU用来激光雷达扫描数据的去畸变，并给出扫描匹配的运动先验信息。然而，IMU并没有涉及到算法的优化过程。因此LOAM可以归类为松耦合方法。文献【7】中提出一种用于地面车辆建图任务的轻量级地面优化激光雷达里程计与建图算法LeGO-LOAM。其对IMU数据的融合过程与LOAM中一致。EKF扩展卡尔曼滤波是另一种更加流行的松耦合融合方法。例如，文献【9】到文献【13】在优化阶段使用EKF结合激光雷达和IMU/GPS观测，来用于机器人状态估计。

Tightly-coupled systems usually offer improved accuracy and are presently a major focus of ongoing research [14]. In [15], preintegrated IMU measurements are exploited for de-skewing point clouds. A robocentric lidar-inertial state estimator, R-LINS, is presented in [16]. R-LINS uses an error-state Kalman filter to correct a robot’s state estimate recursively in a tightly-coupled manner. Due to the lack of other available sensors for state estimation, it suffers from drift during long-during navigation. A tightly-coupled lidar inertial odometry and mapping framework, LIOM, is introduced in [17]. LIOM, which is the abbreviation for LIO-mapping, jointly optimizes measurements from lidar and IMU and achieves similar or better accuracy when compared with LOAM. Since LIOM is designed to process all the sensor measurements, real-time performance is not achieved – it runs at about 0.6×real-time in our tests.

紧耦合系统通常提供更高的精度，并且是目前正在研究的主要热点。文献【15】中，IMU预积分被用到点云去畸变中。在文献【16】中提出一种机器人激光惯导状态估计器RLINS。它以一种紧耦合的方式递归地采用错误状态卡尔曼滤波器去矫正机器人的状态估计。由于缺乏其他用于状态估计的传感器，它在长距离导航过程中容易出现漂移。文献【17】中引入一种紧耦合的激光惯导里程计与建图框架，LIOM。其是LIO-Mapping的缩写，联合优化了激光雷达和IMU的测量结果，与LOAM相比获得了差不多甚至更好的精度。因为LIOM方法被设计用来处理所有的传感器测量值，因此不能达到实时性–在我们的测试中大约跑了六成的实时速度。

四、基于平滑和建图的激光惯导里程计 Lidar Inertial Odometry Via Smoothing and Mapping

1. 系统总览 System Overview

We first define frames and notation that we use throughout the paper. We denote the world frame as W and the robot body frame as B. We also assume the IMU frame coincides with the robot body frame for convenience. The robot state x can be written as:

首先我们定义整个论文中使用的坐标系与变量符号。我们将世界坐标系定义为W，机器人坐标系为B。为了方便起见，我们还假设“IMU坐标系与机器人本体坐标系重合”。机器人的状态x可以写为：

where R ∈SO(3) is the rotation matrix, p ∈R3 is the position vector, v is the speed, and b is the IMU bias. The transformation T ∈SE(3) from B to W is represented as T = [R |p].

其中 R ∈SO(3) 是定义在特殊正交群上的旋转矩阵，p ∈R3  是平移向量，v 是速度，b是IMU的零偏。变换矩阵 T ∈SE(3)  表示从机器人机坐标系  到世界坐标系的特殊欧式群，表示为 T = [R |p]。

An overview of the proposed system is shown in Figure 1. The system receives sensor data from a 3D lidar, an IMU and optionally a GPS. We seek to estimate the state of the robot and its trajectory using the observations of these sensors. This state estimation problem can be formulated as a maximum a posteriori (MAP) problem. We use a factor graph to model this problem, as it is better suited to perform inference when compared with Bayes nets. With the assumption of a Gaussian noise model, the MAP inference for our problem is equivalent to solving a nonlinear least-squares problem [18]. Note that without loss of generality, the proposed system can also incorporate measurements from other sensors, such as elevation from an altimeter or heading from a compass.

图 1 显示了所提出的系统的概览。该系统从激光雷达、IMU以及可选的GPS中接收传感器数据。我们试图利用这些传感器的观测来估计机器人的状态及其轨迹。状态估计问题可以表示为一个最大后验MAP问题。我们使用因子图去建模这个问题，因为与贝叶斯网络相比，因子图更适合执行推理任务。在高斯噪声模型的假设下，我们问题的最大后验估计等价于求解一个非线性最小二乘问题。注意，如果不失一般性，我们提出的系统还可以包含来自其他传感器的测量，比如高度计的海拔高度以及指南针的航向等。

We introduce four types of f actors along with one variable type for factor graph construction. This variable, representing the robot’s state at a specific time, is attributed to the nodes of the graph. The four types of factors are:

• (a) IMU preintegration factors,
• (b) lidar odometry factors,
• (c) GPS factors,
• (d) loop closure factors.

A new robot state node x is added to the graph when the change in robot pose exceeds a user-defined threshold. The factor graph is optimized upon the insertion of a new node using incremental smoothing and mapping with the Bayes tree (iSAM2) [19]. The process for genera

我们介绍四种类型的因子factors，以及一种因子图构造的变量类型variable。该变量表示机器人状态在特定时间的状态归属于因子图中的节点nodes。这四种因子分别是：

• (a) IMU预积分因子
• (b) 激光雷达里程计因子
• (c) GPS因子
• (d) 闭环因子

当机器人姿态的变化超过用户定义的阈值时，图中会添加一个新的机器人状态节点  。在使用贝叶斯树（iSAM2）增量式平滑和建图过程插入一个新的节点时，因子图会随之进行优化。

2. IMU预积分因子 IMU Preintegration Factor

The measurements of angular velocity and acceleration from an IMU are defined using Eqs. 2 and 3:

IMU角速度和加速度的观测公式定义如下：

whereˆωt and ˆat are the raw IMU measurements in B at time t. ˆωt and ˆat are affected by a slowly varying bias bt and white noise nt. RBWt is the rotation matrix from W to B. g is the constant gravity vector in W.

其中 ˆωt 和 ˆat 是机体坐标系下 t 时刻的IMU观测源数据。ˆωt 和 ˆat 均受到缓慢变化的IMU零偏 bt 以及白噪声 nt 的影响。 RBWt 是从世界坐标系到机体坐标系的旋转矩阵。t  是世界坐标系  W 下的重力常数向量。

We can now use the measurements from the IMU to infer the motion of the robot. The velocity, position and rotation of the robot at time t + ∆t can be computed as follows:

现在我们可以采用IMU测量去推断出机器人的运动。机器人在 t + ∆t 时刻的速度、位置以及旋转计算如下：

where Rt = RWB t = RtBW T. Here we assume that the t angular velocity and the acceleration of B remain constant during the above integration.

其中  Rt = RWB t = R t BW T。这里我们假设机器人角速度和加速度在积分过程中保持匀速不变。

We then apply the IMU preintegration method proposed in [20] to obtain the relative body motion between two timesteps. The preintegrated measurements ∆vij , ∆pij , and ∆Rij between time i and j can be computed using:

然后我们采用文献【20】提出的IMU预积分去获取两个时间戳之间的相对运动。预积分得到的第 i 和第 j 时刻之间的速度测量 ∆vij、位置测量 ∆pij 以及旋转测量 ∆Rij 计算如下：

Due to space limitations, we refer the reader to the de- scription from [20] for the detailed derivation of Eqs. 7 – 9. Besides its efficiency, applying IMU preintegration also naturally gives us one type of constraint for the factor graph – IMU preintegration factors. The IMU bias is jointly optimized alongside the lidar odometry factors in the graph.

由于篇幅限制，我们让读者参考来自文献【20】的描述，来得到公式【2-9】的详细推导。除了IMU预积分的效率之外，应用IMU预积分也可以很自然地给出IMU预积分因子在因子图中的约束条件。IMU零偏因子与激光雷达里程计因子在因子图中一起进行联合优化。

3.激光雷达里程计因子 Lidar Odometry Factor

When a new lidar scan arrives, we first perform fea- ture extraction. Edge and planar features are extracted by evaluating the roughness of points over a local region. Points with a large roughness value are classified as edge features. Similarly, a planar feature is categorized by a small roughness value. We denote the extracted edge and planar features from a lidar scan at time i as Fei and Fpi respectively. All the features extracted at time i compose a lidar frame Fi, where Fi = {Fei , Fpi }. Note that a lidar frame F is represented in B. A more detailed description of the feature extraction process can be found in [1], or [7] if a range image is used.

当新的一圈激光雷达扫描到来时，首先执行特征提取。通过评估局部区域上点的粗糙度/曲率来提取边缘和平面特征。粗糙度/曲率较大的点被划分为边缘特征。类似地，一个平面特征也可以按一个小的粗糙度/曲率进行分类。 我们将从激光雷达在 t 时刻扫描点云中提取的边缘特征以及平面特征分别定义为 Fei 以及 Fpi。在 t 时刻提取的所有特征构成了一个激光雷达点云帧  Fi，其中 Fi = {Fei , Fpi } 。注意一个激光雷达点云帧 F 是表示在机器人坐标系下的。特征提取步骤的更多详细描述可以在文献【1】或如果用到距离图像也可以参考文献【7】。

Using every lidar frame for computing and adding factors to the graph is computationally intractable, so we adopt the concept of keyframe selection, which is widely used in the visual SLAM field. Using a simple but effective heuristic approach, we select a lidar frame Fi+1 as a keyframe when the change in robot pose exceeds a user-defined threshold when compared with the previous state xi. The newly saved keyframe, Fi+1, is associated with a new robot state node, xi+1, in the factor graph. The lidar frames between two keyframes are discarded. Adding keyframes in this way not only achieves a balance between map density and memory consumption but also helps maintain a relatively sparse factor graph, which is suitable for real-time nonlinear optimization. In our work, the position and rotation change thresholds for adding a new keyframe are chosen to be 1m and 10◦ .

如果将每一帧激光雷达点云都拿来计算因子并添加到因子图中是难以计算的，因此我们采用了关键帧选择的概念，其被广泛应用于视觉SLAM领域。使用一种简单但有效的启发式方法，当机器人姿态的变化与先前的状态相比，如果超过了用户定义的阈值时，我们选择此时的激光雷达帧作为关键帧。新保存的关键帧 与因子图的中新的机器人状态节点相关联。然后丢弃掉两个关键帧之间的其他激光雷达帧。这样添加的关键帧不仅可以实现地图密度和内存消耗之间的平衡，而且有助于保持一个相对稀疏的因子图结构，适用于实时的非线性优化。在我们的工作中，添加新关键帧的平移和旋转的变化阈值选择为1米和10度。

Let us assume we wish to add a new state node xi+1 to the factor graph. The lidar keyframe that is associated with this state is Fi+1. The generation of a lidar odometry factor is described in the following steps:

假设我们希望在因子图中添加一个新的状态节点  xi+1。那么与该状态相关联的激光雷达关键帧为  Fi+1。激光雷达里程计因子的生成过程描述如下：

a）建立子关键帧的体素地图 Sub-keyframes for voxel map

We implement a sliding window approach to create a point cloud map containing a fixed number of recent lidar scans. Instead of optimizing the transformation between two consecutive lidar scans, we extract the n most recent keyframes, which we call the sub-keyframes, for estimation. The set of sub-keyframes {Fi−n, …, Fi}is then transformed into frame W using the transformations {Ti−n, …, Ti}associated with them. The transformed sub-keyframes are merged together into a voxel map Mi. Since we extract two types of features in the previous feature extraction step, Mi is composed of two sub- voxel maps that are denoted Mei , the edge feature voxel map, and Mpi , the planar feature voxel map. The lidar frames and voxel maps are related to each other as follows:

我们实现了一种滑动窗口方法去构建点云地图，其中包含了固定数目的最近激光雷达的扫描点云。我们没有优化两个连续的激光雷达扫描点云帧之间的变换关系，而是提取了n个最近的关键帧，sub-keyframes子关键帧，来进行估计。采用变换关系{Ti−n, …, Ti} 将关联的子关键帧集合{Fi−n, …, Fi} 转换到世界坐标系中。转换后的子关键帧会被合并成一个体素地图Mi。由于我们在之前的特征提取步骤中提取了两种特征：边缘特征以及平面特征，因此体素地图Mi 由两个子体素地图构成，定义边缘特征体素地图为Mei，平面特征体素地图为Mpi。激光雷达帧以及体素地图之间的关系如下：

′Fei and ′Fpi are the transformed edge and planar features in W. Mei and Mpi are then downsampled to eliminate the duplicated features that fall in the same voxel cell. In this paper, n is chosen to be 25. The downsample resolutions for Me i and Mp i are 0.2m and 0.4m, respectively.

而 ′Fei 和 ′Fpi  是转换到世界坐标系下的边缘特征和平面特征。然后对子体素地图 Mei 和 Mpi 进行下采样，消除落在同一个体素单元中的重复冗余特征。本文中，n 选择25。Mei 和 Mpi 下采样的分辨率分别设为0.2m和0.4m。

b）扫描匹配 Scan-matching

We match a newly obtained lidar frame Fi+1, which is also {Fei+1, Fpi+1}, to Mi via scan- matching. Various scan-matching methods, such as [3] and [4], can be utilized for this purpose. Here we opt to use the method proposed in [1] due to its computational efficiency and robustness in various challenging environments.

我们将新获得的激光雷达关键帧 Fi+1 = {Fei+1, Fpi+1} 通过扫描匹配到世界坐标系下的体素地图 Mi 中。为此，可以使用各种扫描匹配scan-match方法，比如ICP【3】和GICP【4】。这里，我们选择使用文献【1】中提出的方法，因为它具备出色计算效率和在各种有挑战性的环境中有很好的鲁棒性。

We first transform {Fe i+1, Fp i+1}from B to W and obtain {′Fe ′Fp i+1, i+1}. This initial transformation is obtained by using the predicted robot motion,˜ Ti+1, from the IMU. For each feature in ′Fe i+1 or ′Fp i+1, we then find its edge or planar correspondence in Me i or Mp i . For the sake of brevity, the detailed procedures for finding these correspondences are omitted here, but are described thoroughly in [1].

我们首先将激光雷达关键帧 {Fe i+1, Fp i+1} 从机器人坐标系转换到世界坐标系中，得到转换后的关键帧集合为  {′Fe ′Fp i+1, i+1}。初始的变换关系是通过从IMU预测的机器人运动 ˜ Ti+1 中得到的。对于每帧 ′Fe i+1 或 ′Fp i+1 中的边缘特征和平面特征，我们然后找到它们对应的子体素地图 Mei 和 Mpi 中的边缘和平面。为了简洁起见，找到对应关系的详细过程在这里省略，文献【1】中给出了详细的描述。

c）相对变换关系 Relative transformation

The distance between a fea- ture and its edge or planar patch correspondence can be computed using the following equations:

边缘特征与平面特征和它们对应的边缘或平面块之间的距离可以通过如下的公式进行计算：

where k, u, v, and w are the feature indices in their corresponding sets. For an edge feature pei+1,k in ′Fei+1, pei,u and pei,v are the points that form the corresponding edge line in Mei . For a planar feature ppi+1,k in ′Fpi+1, ppi,u, ppi,v , and ppi,w form the corresponding planar patch in Mpi . The GaussNewton method is then used to solve for the optimal transformation by minimizing:

其中，k, u, v, w  是在边缘特征或平面特征对应集合中的索引号。对于在转换后的边缘关键帧 ′Fe i+1 中的边缘特征 pe i+1,k  来说，pei,u 和 pei,v  是形成边缘子体素地图 Mei 中相对应的边缘线上的点。而对于在转换后的平面关键帧 ′Fpi+1 中的平面特征 ppi+1,k 来说，ppi,u, ppi,v 以及 ppi,w 形成了平面子体素地图 Mpi 中对应的平面块。然后采用高斯牛顿法来求解最优的变换矩阵关系，通过最小化下述公式：

At last, we can obtain the relative transformation ∆Ti,i+1 between xi and xi+1, which is the lidar odometry factor linking these two poses:

最后，我们可以得到状态节点 xi 与状态节点 xi+1 之间的相对变换关系 ∆Ti,i+1，它是连接这两种位姿的激光里程计因子：

 

We note that an alternative approach to obtain ∆Ti,i+1 is to transform sub-keyframes into the frame of xi. In other words, we match Fi+1 to the voxel map that is represented in the frame of xi. In this way, the real relative transformation ∆Ti,i+1 can be directly obtained. Because the transformed features ′Fei and ′Fpi can be reused multiple times, we instead opt to use the approach described in Sec. III-C.1 for its computational efficiency.

我们注意到，获得 ∆Ti,i+1 的另一种方法是将子关键帧转换到 xi 状态节点的坐标系下。换句话说，就是将 Fi+1 与在 xi 状态节点坐标系下表示的体素地图进行匹配。这种方式下，可以直接得到实施相对变换关系  ∆Ti,i+1。由于转换后的特征 ′Fei 和 ′Fpi  可以多次重复使用，所以我们选择采用第III节-C.1中描述的方法，因为它的计算效率很高。

4. GPS 因子 GPS Factor

Though we can obtain reliable state estimation and map- ping by utilizing only IMU preintegration and lidar odometry factors, the system still suffers from drift during long- duration navigation tasks. To solve this problem, we can introduce sensors that offer absolute measurements for elim- inating drift. Such sensors include an altimeter, compass, and GPS. For the purposes of illustration here, we discuss GPS, as it is widely used in real-world navigation systems.

虽然仅仅利用IMU预积分和激光里程计因子就可以获得可靠的状态估计以及建图，但是这个系统在长期的导航任务中，仍然存在漂移问题。为了解决这个问题，我们可以引入提供消除漂移的绝对测量值的传感器。这些传感器包括高度计、指南针罗盘以及GPS全球定位系统。这里为了阐述清楚，我们讨论了其中GPS，因为它在现实导航系统中被广泛使用。

When we receive GPS measurements, we first transform them to the local Cartesian coordinate frame using the method proposed in [21]. Upon the addition of a new node to the factor graph, we then associate a new GPS factor with this node. If the GPS signal is not hardware-synchronized with the lidar frame, we interpolate among GPS measurements linearly based on the timestamp of the lidar frame.

当我们接收GPS测量时，首先使用文献【21】中提到的方法将GPS坐标转换到局部笛卡尔坐标系下。在因子图中添加一个新的节点后，我们将新的GPS因子和这个新节点关联起来。如果GPS信号与激光雷达没有做硬件同步，那么我们根据激光雷达的时间戳在GPS中进行线性插值。

We note that adding GPS factors constantly when GPS reception is available is not necessary because the drift of lidar inertial odometry grows very slowly. In practice, we only add a GPS factor when the estimated position covariance is larger than the received GPS position covariance.

我们注意到，当GPS接收可用时，不断添加GPS因子是没有必要的，因为激光惯导里程计漂移增加是非常缓慢的。在实践中，我们只需要在估计的位置协方差大于接收到的GPS位置协方差的时候，才去增加一个GPS因子。

5. 闭环因子 Loop Closure Factor

Thanks to the utilization of a factor graph, loop closures can also be seamlessly incorporated into the proposed system, as opposed to LOAM and LIOM. For the purposes of illustration, we describe and implement a naive but effective Euclidean distance-based loop closure detection approach. We also note that our proposed framework is compatible with other methods for loop closure detection, for example, [22] and [23], which generate a point cloud descriptor and use it for place recognition.

由于利用了因子图，闭环也可以无缝地插入到提出的系统中，而不是跟LOAM和LIO Mapping那样。为了说明，我们描述并实现了一种朴素但有效的基于欧氏距离的闭环检测方法。我们还注意到，我们提出的框架与其他的闭环检测方法是兼容的，例如文献【22】【23】提到的方法，他们生产了一个点云描述符并将它用于位置识别。

When a new state xi+1 is added to the factor graph, we first search the graph and find the prior states that are close to xi+1 in Euclidean space. As is shown in Fig. 1, for example, x3 is one of the returned candidates. We then try to match Fi+1 to the sub-keyframes {F3−m, …, F3, …, F3+m}using scan-matching. Note that Fi+1 and the past sub-keyframes are first transformed into W before scan-matching. We obtain the relative transformation ∆T3,i+1 and add it as a loop closure factor to the graph. Throughout this paper, we choose the index m to be 12, and the search distance for loop closures is set to be 15m from a new state xi+1.

当一个新的状态 xi+1 被加入到因子图中，我们首先在因子图中进行搜索，找到欧式空间中接近状态 xi+1 的先验状态。如图1所示，状态节点 x3 是其中一个返回的候选对象。然后我们尝试用扫描匹配scan-match方式将关键帧 Fi+1 与子关键帧集 {F3−m, …, F3, …, F3+m} 进行匹配。注意，关键帧 Fi+1 和过去的子关键帧在扫描匹配scan-match之前已经先被转换到世界坐标系W中 。然后我们就得到了相对变换 ∆T3,i+1 ，并将其作为一个闭环因子添加到因子图中。在本文中，我们选择索引数m为12，闭环与新状态 xi+1 的搜索范围设为15m。

In practice, we find adding loop closure factors is espe- cially useful for correcting the drift in a robot’s altitude, when GPS is the only absolute sensor available. This is because the elevation measurement from GPS is very inaccurate – giving rise to altitude errors approaching 100m in our tests, in the absence of loop closures.

实际中，我们发现，当GPS是唯一可用的绝对位置测量传感器的时候，添加闭环因子对于修正机器人高程上的漂移特别有用。这是由于GPS的高程测量是非常不准确的，在我们的测试中，没有闭环情况下，会导致接近100米的高程误差。

五、实验 Experiments

We now describe a series of experiments to qualitatively and quantitatively analyze our proposed framework. The sensor suite used in this paper includes a Velodyne VLP- 16 lidar, a MicroStrain 3DM-GX5-25 IMU, and a Reach M GPS. For validation, we collected 5 different datasets across various scales, platforms and environments. These datasets are referred to as Rotation, Walking, Campus, Park and Amsterdam, respectively. The sensor mounting platforms are shown in Fig. 2. The first three datasets were collected using a custom-built handheld device on the MIT campus. The Park dataset was collected in a park covered by vegetation, using an unmanned ground vehicle (UGV) – the Clearpath Jackal. The last dataset, Amsterdam, was collected by mounting the sensors on a boat and cruising in the canals of Amsterdam. The details of these datasets are shown in Table I.

我们现在描述一系列的实验来定性和定量地分析我们提出的框架。本文采用的传感器套件包括一个Velodyne16线激光雷达，一个MicroStrain 3DM-GX5-25的IMU以及一个Reach M的GPS。为了进行实验验证，我们在不同尺度、平台和环境中搜集了5个不同的数据集。这些数据集分别为Rotation，Walking，Campus，Park，Amsterdam。传感器安装平台如图2所示。

前三个数据集是使用MIT校园里定制的手持式设备搜集的。Park数据集是在一个植被覆盖的公园里采集的，使用了一辆无人地面车辆（UGV）- Clearpath Jackal。最后一个数据集，Amsterdam，是通过将传感器安装在一艘电动船上，并在阿姆斯特丹运河中巡航采集的。这些数据集的详细信息显示在下表中。

数据集	扫描数	高程变化(米)	轨迹长度(米)	最大旋转速度(度/秒)
Rotation	582	0	0	213.9
Walking	6502	0.3	801	133.7
Campus	9865	1.0	1437	124.8
Park	24691	19.0	2898	217.4
Amsterdam	107656	0	19065	17.2

We compare the proposed LIO-SAM framework with LOAM and LIOM. In all the experiments, LOAM and LIO- SAM are forced to run in real-time. LIOM, on the other hand, is given infinite time to process every sensor measurement. All the methods are implemented in C++ and executed on a laptop equipped with an Intel i7-10710U CPU using the robot operating system (ROS) [24] in Ubuntu Linux. We note that only the CPU is used for computation, without parallel computing enabled. Our implementation of LIO-SAM is freely available on Github1. Supplementary details of the experiments performed, including complete visualizations of all tests, can be found at the link below2 .

我们将提出的LIO-SAM框架与LOAM和LIO Mapping进行比较。在所有实验中，LOAM和LIO-SAM实时的运行了。而LIO-Mapping相反，给了无限多的时间来处理每个传感器的观测值。所有的方法都在C++中实现，并在配备了Intel i7-10710U CPU的笔记本上运行，使用的平台是是Ubuntu中的ROS机器人操作系统。我们注意到，只有CPU适用于计算，没有启用并行计算。我们的LIO-SAM的实现可以在我们的Github中进行下载。执行实验的补充细节，包括所有测试的完整视频，可以在我们的YouTube频道中找到

1. Rotation数据集

In this test, we focus on evaluating the robustness of our framework when only IMU preintegration and lidar odometry factors are added to the factor graph. The Rotation dataset is collected by a user holding the sensor suite and performing a series of aggressive rotational maneuvers while standing still. The maximum rotational speed encountered in this test is 133.7 ◦/s. The test environment, which is populated with structures, is shown in Fig. 3(a). The maps obtained from LOAM and LIO-SAM are shown in Figs. 3(b) and (c) respec- tively.

在这个测试中，当只使用IMU预积分以及激光里程计因子被添加到因子图中时，重点评估我们提出的LIO-SAM框架的鲁棒性。Rotation数据集是人手持传感器套件采集的，在原地静止不移动条件下，只进行纯旋转操作。本实验中最大的旋转速度为133.7度每秒。测试环境如图3(a)所示。LOAM和LIO-SAM中生成的地图如图3(b)，图3(c)所示。

图3. LOAM和LIO-SAM在Rotation纯旋转数据集上的建图结果。LIO-Mapping没有建出好结果。

Because LIOM uses the same initialization pipeline from [25], it inherits the same initialization sensitivity of visual-inertial SLAM and is not able to initialize properly using this dataset. Due to its failure to produce meaningful results, the map of LIOM is not shown. As is shown, the map of LIO-SAM preserves more fine structural details of the environment compared with the map of LOAM. This is because LIO-SAM is able to register each lidar frame precisely in SO(3), even when the robot undergoes rapid rotation.

由于LIO-Mapping使用了文献【25】中相同的初始化过程，继承了视觉惯导SLAM类似的对初始化的敏感性，并且无法使用这个Rotation数据完成正确的初始化。由于LIO-Maping没能产生有意义的结果，它的地图就没有显示出来。从图中可以看出，与LOAM算法相比，LIO-SAM构建的地图保留了更精细的环境结构细节。这是由于LIO-SAM能够在SO(3)特殊正交群中精确的注册每个激光雷达帧点云，即使当机器人发生了快速旋转的情况下。

2. Walking数据集

This test is designed to evaluate the performance of our method when the system undergoes aggressive translations and rotations in SE(3). The maximum translational and rotational speed encountered is this dataset is 1.8 m/s and 213.9 ◦/s respectively. During the data gathering, the user holds the sensor suite shown in Fig. 2(a) and walks quickly across the MIT campus (Fig. 4(a)). In this test, the map of LOAM, shown in Fig. 4(b), diverges at multiple locations when aggressive rotation is encountered. LIOM outperforms LOAM in this test. However, its map, shown in Fig. 4(c), still diverges slightly in various locations and consists of numerous blurry structures. Because LIOM is designed to process all sensor measurements, it only runs at 0.56×real- time while other methods are running in real-time. Finally, LIO-SAM outperforms both methods and produces a map that is consistent with the available Google Earth imagery.

这个测试设计的目的在于评估我们提出的方法在SE(3)特殊欧式群中系统发生剧烈平移和旋转的情况下的性能。这个数据集上遇到的最大平移速度和旋转速度分别为1.8米每秒和213.9度每秒。在数据采集期间，人拿着图2(a)那样的手持式传感器，然后快速行走在MIT校园中，如图4(a)中。这个实验中，LOAM建的地图，如图4(b)所示，当遇到主动旋转时候，会在多个位置出现发散。LIO-Mapping在这个数据集上要比LOAM表现的出色。然而LIO-Mapping建的地图，如图4(c)所示，在不同位置仍然存在不一样，并且由很多模糊的结构组成。由于LIO-Mapping被设计用来处理所有传感器的测量，因此它旨在0.56倍的实时条件下运行，而其他两种方法都可以实时运行。最后，LIO-SAM的性能要优于其他两种方法，并构建了一张与可用的谷歌地图一致的地图。

3. Campus数据集

This test is designed to show the benefits of introducing GPS and loop closure factors. In order to do this, we purposely disable the insertion of GPS and loop closure factors into the graph. When both GPS and loop closure factors are disabled, our method is referred to as LIO-odom, which only utilizes IMU preintegration and lidar odometry factors. When GPS factors are used, our method is referred to as LIO-GPS, which uses IMU preintegration, lidar odometry, and GPS factors for graph construction. LIO-SAM uses all factors when they are available.

本数据集上的测试是设计用来展示引入GPS 和 闭环因子后的建图效果。为了做到这一点，我们故意未添加GPS和闭环因子到因子图中。当GPS和闭环因子禁用后，我们提出的方法命名为LIO-Odom，也就是只利用IMU预积分和激光里程计因子。当使用GPS因子时，我们提出的方法定义为LIO-GPS，其使用IMU预积分，激光里程计以及GPS因子用于建图。LIO-SAM则是在图中添加了所有的因子。

To gather this dataset, the user walks around the MIT campus using the handheld device and returns to the same position. Because of the numerous buildings and trees in the mapping area, GPS reception is rarely available and inaccu- rate most of the time. After filtering out the inconsistent GPS measurements, the regions where GPS is available are shown in Fig. 5(a) as green segments. These regions correspond to the few areas that are not surrounded by buildings or trees.

为了收集这个数据集，研究人员使用手持式传感器设备在MIT校园周围走动，并返回到相同位置。由于在建图区域存在许多建筑物和树木，GPS接收几乎不可用，而且大多数时候也不准确。在过滤掉不一致的GPS观测后，可用的GPS如图5(a)绿色部分所示。这些区域对应于少数没有建筑物或树木包围的区域。

The estimated trajectories of LOAM, LIO-odom, LIO- GPS, and LIO-SAM are shown in Fig. 5(a). The results of LIOM are not shown due to its failure to initialize properly and produce meaningful results. As is shown, the trajectory of LOAM drifts significantly when compared with all other methods. Without the correction of GPS data, the trajectory of LIO-odom begins to visibly drift at the lower right corner of the map. With the help of GPS data, LIO-GPS can correct the drift when it is available. However, GPS data is not available in the later part of the dataset. As a result, LIO- GPS is unable to close the loop when the robot returns to the start position due to drift. On the other hand, LIO- SAM can eliminate the drift by adding loop closure factors to the graph. The map of LIO-SAM is well-aligned with Google Earth imagery and shown in Fig. 5(b). The relative translational error of all methods when the robot returns to the start is shown in Table II.

LOAM、LIO-Odom、LIO-GPS以及LIO-SAM估计出来的轨迹如图5(a)所示。由于LIO-Mapping没能正确地初始化，并且未能产生有意义的结果，因此LIO-Mapping的结果没有展示出来。如图上所示，和其他其他方法相比，LOAM的轨迹有明显的漂移。由于没有对GPS数据进行修正，在地图的右下角LIO-Odom的轨迹开始出现明显的漂移。加入了GPS数据后，LIO-GPS可以在GPS可用时修正漂移。但是，在数据集的后半部分GPS都是不可用的。因此，当由于漂移导致机器人返回到起始位置时，LIO-GPS无法检测到闭环。另一方面，LIO-SAM可以通过向因子图中添加闭环因子来消除轨迹漂移。LIO-SAM建的地图与谷歌地球上的图可以很好的对齐，如图5(b)所示。当机器人回到原点时，所有方法的相对平移误差如下表所示。

数据集	LOAM	LIOM	LIO-Odom	LIO-GPS	LIO-SAM
Campus	192.43	Fail	9.44	6.87	0.12
Park	121.74	34.60	36.36	2.93	0.04
Amsterdam	Fail	Fail	Fail	1.21	0.17

4. Park 数据集

In this test, we mount the sensors on a UGV and drive the vehicle along a forested hiking trail. The robot returns to its initial position after 40 minutes of driving. The UGV is driven on three road surfaces: asphalt, ground covered by grass, and dirt-covered trails. Due to its lack of suspension, the robot undergoes low amplitude but high frequency vibra- tions when driven on non-asphalt roads.

在本次测试中，我们将传感器安装在一辆UGV无人车上，沿着森林徒步路线行驶。机器人在行驶40分钟后回到出发位置。无人车在三种路面上行驶：沥青路面、草坪以及泥地。由于缺乏悬挂系统，这个机器人在非沥青路面行驶过程中，会出现低幅度高频率的振动。

To mimic a challenging mapping scenario, we only use GPS measurements when the robot is in widely open areas, which is indicated by the green segments in Fig. 6(a). Such a mapping scenario is representative of a task in which a robot must map multiple GPS-denied regions and periodically returns to regions with GPS availability to correct the drift.

为了模拟具有挑战性的建图场景，我们只在机器人处于开放的区域时使用GPS测量值，比如图6(a)中的绿色部分。这种建图场景一类任务的代表，即机器人必须在没有GPS的区域进行建图，并定期返回有GPS信号的区域来纠正漂移。

Similar to the results in the previous tests, LOAM, LIOM, and LIO-odom suffer from significant drift, since no absolute correction data is available. Additionally, LIOM only runs at 0.67×real-time, while the other methods run in real-time. Though the trajectories of LIO-GPS and LIO-SAM coincide in the horizontal plane, their relative translational errors are different (Table II). Because no reliable absolute elevation measurements are available, LIO-GPS suffers from drift in altitude and is unable to close the loop when returning to the robot’s initial position. LIO-SAM has no such problem, as it utilizes loop closure factors to eliminate the drift.

与前面实验结果类似，LOAM、LIO-Mapping和LIO-Odom都出现了很明显的轨迹漂移，因为他们没有使用绝对校正数据。此外，LIO-Mapping只在0.67倍实时速度下运行，而其他方法是实时运行的。虽然LIO-GPS和LIO-SAM的轨迹在水平面保持一致，但它们的相对平移误差是不一样的如表II所示。由于没有可靠的绝对高度测量值，LIO-GPS在高度上有漂移，并且在返回到机器人的起始位置时无法闭环。LIO-SAM没有出现这样的问题，因为它利用闭环因子来消除轨迹漂移。

5. Amsterdam 数据集

Finally, we mounted the sensor suite on a boat and cruised along the canals of Amsterdam for 3 hours. Although the movement of the sensors is relatively smooth in this test, mapping the canals is still challenging for several reasons. Many bridges over the canals pose degenerate scenarios, as there are few useful features when the boat is under them, similar to moving through a long, featureless corridor. The number of planar features is also significantly less, as the ground is not present. We observe many false detections from the lidar when direct sunlight is in the sensor field-of-view, which occurs about 20% of the time during data gathering. We also only obtain intermittent GPS reception due to the presence of bridges and city buildings overhead.

最后，我们把传感器套件安装到电动船上，沿着阿姆斯特丹的运河巡航3小时。虽然在这次测试中，传感器的移动相对平稳，但由于存在若干个原因，给运河整体建图仍然具有挑战性。运河上的许多桥梁都出现了退化的情况，因为当船出现在桥下时，几乎没有什么有用的特征，类似于穿过一条很长又毫无特色的走廊。由于水里不存在地面，平面特征的数量也明显较少。当阳光直射到传感器的视野范围内时，我们观察到许多激光雷达的错误检测，这发生在数据采集总时长的20%处。由于电动船上方桥梁和城市建筑的存在，我们也只获得了间歇性的GPS信号的接收。

Due to these challenges, LOAM, LIOM, and LIO-odom all fail to produce meaningful results in this test. Similar to the problems encountered in the Park dataset, LIO-GPS is unable to close the loop when returning to the robot’s initial position because of the drift in altitude, which further motivates our usage of loop closure factors in LIO-SAM.

由于存在这样那样的挑战，LOAM、LIO-Mapping和LIO-Odom都未能在这个测试中产生有意义的结果。与Park公园数据集中遇到的问题类似，LIO-GPS由于高度值上出现漂移，在返回机器人的初始位置时无法闭环，这进一步激发我们在LIO-SAM中使用闭环因子来消除轨迹上的漂移。

6. 基准测试结果 Benchmarking Results

Since full GPS coverage is only available in the P ark dataset, we show the root mean square error (RMSE) results w.r.t to the GPS measurement history, which is treated as ground truth. This RMSE error does not take the error along the z axis into account. As is shown in Table III, LIO-GPS and LIO-SAM achieve similar RMSE error with respect to the GPS ground truth. Note that we could further reduce the error of these two methods by at least an order of magni- tude by giving them full access to all GPS measurements. However, full GPS access is not always available in many mapping settings. Our intention is to design a robust system that can operate in a variety of challenging environments.

由于完整的GPS覆盖只在Park数据集中可用，因此我们显示了关于GPS测量历史的均方根误差(RMSE)结果，可以把它看作Ground Truth真值。这里均方根误差没有考虑沿z轴发生的误差。如下表所示，LIO-GPS和LIO-SAM在GPS的Ground Truth真值上都达到了差不多的RMSE均方根误差。需要注意的是，我们可以通过让这两种方法使用所有GPS测量值，来使其均RMSE方根误差减少至少一个数量级。然而，在许多建图配置中，完整GPS观测并不总是可用的。我们的目的是设计一个可以在各种具有挑战性的环境中都可运行的鲁棒系统。

数据集	LOAM	LIOM	LIO-Odom	LIO-GPS	LIO-SAM
Park	47.31	28.96	23.96	1.09	0.96

The average runtime for the three competing methods to register one lidar frame across all five datasets is shown in Table IV. Throughout all tests, LOAM and LIO-SAM are forced to run in real-time. In other words, some lidar frames are dropped if the runtime takes more than 100ms when the lidar rotation rate is 10Hz. LIOM is given infinite time to process every lidar frame. As is shown, LIO-SAM uses significantly less runtime than the other two methods, which makes it more suitable to be deployed on low-power embedded systems.

LOAM、LIO-Mapping以及LIO-SAM这三种对比方法，在上述5个数据集上处理一个激光雷达点云帧的平均运行时间如下表所示。在所有测试中，LOAM和LIO-SAM是实时运行的。换句话说，当激光雷达的旋转速率为10Hz时，如果运行时间需要超过100ms，那么一些激光雷达帧点云就会被丢弃。我们给LIO-Mapping方法无限长的时间来处理每个激光雷达帧。如图中所示，LIO-SAM的运行时间明显少于其他两种方法，这使得它更适合部署在低功耗的嵌入式系统上。

数据集	LOAM	LIOM	LIO-SAM	Stress Test
Rotation	83.6	Fail	41.9	13x
Walking	253.6	339.8	58.4	13x
Campus	244.9	Fail	97.8	10x
Park	266.4	245.2	100.5	9x
Amsterdam	Fail	Fail	79.3	11x

We also perform stress tests on LIO-SAM by feeding it the data faster than real-time. The maximum data playback speed is recorded and shown in the last column of Table IV when LIO-SAM achieves similar performance without failure compared with the results when the data playback speed is 1×real-time. As is shown, LIO-SAM is able to process data faster than real-time up to 13×.

我们还通过比实时速度更快的输入数据到LIO-SAM中，对其进行压力测试。当LIO-SAM在加速播放与1倍速回放数据的结果进行比较，可以顺利达到相似的性能时，记录下最大数据回放速度并显示在上表的最后一列中。从图中可以看出，LIO-SAM能够以高达13倍速来处理数据。

We note that the runtime of LIO-SAM is more signif- icantly influenced by the density of the feature map, and less affected by the number of nodes and factors in the factor graph. For instance, the Park dataset is collected in a feature-rich environment where the vegetation results in a large quantity of features, whereas the Amsterdam dataset yields a sparser feature map. While the factor graph of the Park test consists of 4,573 nodes and 9,365 factors, the graph in the Amsterdam test has 23,304 nodes and 49,617 factors. Despite this, LIO-SAM uses less time in the Amsterdam test as opposed to the runtime in the Park test.

我们注意到，LIO-SAM的运行时间明显会受到特征地图密度的影响，但受到因子图中节点数和因子数的影响比较小。例如，Park数据集是在一个特征丰富的环境中采集的，其中的绿植产生了大量的特征，而Amsterdam数据集产生的特征地图相对更稀疏。Park数据集实验中的因子图包含4573个节点和9365个因子，而Amsterdam数据集实验中的因子图则有23304个节点和49617个因子。尽管如此，与Park数据集测试相比，LIO-SAM在Amsterdam数据集测试中使用的时间更少。

图 7：LIO-SAM 与 Google Earth 对齐的地图。

六、结论与讨论 Conclusion and Discussion

We have proposed LIO-SAM, a framework for tightly- coupled lidar inertial odometry via smoothing and mapping, for performing real-time state estimation and mapping in complex environments. By formulating lidar-inertial odom- etry atop a factor graph, LIO-SAM is especially suitable for multi-sensor fusion. Additional sensor measurements can easily be incorporated into the framework as new factors. Sensors that provide absolute measurements, such as a GPS, compass, or altimeter, can be used to eliminate the drift of lidar inertial odometry that accumulates over long durations, or in feature-poor environments. Place recognition can also be easily incorporated into the system. To improve with_gateway_unit real-time performance of the system, we propose a sliding window approach that marginalizes old lidar frames for scan- matching. Keyframes are selectively added to the factor graph, and new keyframes are registered only to a fixed- size set of sub-keyframes when both lidar odometry and loop closure factors are generated. This scan-matching at a local scale rather than a global scale facilitates the real- time performance of the LIO-SAM framework. The proposed method is thoroughly evaluated on datasets gathered on three platforms across a variety of environments. The results show that LIO-SAM can achieve similar or better accuracy when compared with LOAM and LIOM. Future work involves testing the proposed system on unmanned aerial vehicles.

我们提出了LIO-SAM，一个通过平滑和建图实现紧耦合激光雷达惯性里程计框架，用于复杂环境中执行实时状态估计和建图。通过在因子图上建立激光雷达-惯性里程计，LIO-SAM特别适用于多传感器融合。额外的传感器测量值可以很容易地作为新的因子加入到框架中。提供绝对测量的传感器，比如GPS、罗盘指南盘或高度计，可以用来消除激光雷达惯性里程计在长时间运行或特征比较少的环境中累计的轨迹漂移。位置识别也可以很容易地融入到系统中。为了提高系统的实时性能，我们提出了一种滑动窗口方法，边缘化旧的激光雷达帧进行scan-matching扫描匹配。关键帧被有选择性地添加到因子图中，并且当同时产生激光雷达里程计因子和闭环因子时，新的关键帧只关联到固定大小的子关键帧集中。这种局部尺度而不是全局尺度的scan-match扫描匹配方法提高了LIO-SAM算法框架的实时性能。提出的LIO-SAM方法在不同环境的三个移动平台中采集的数据集上进行了全面的评估。结果表明，与LOAM和LIO-Mapping相比，LIO-SAM可以获得相似或更好的精度。未来的工作包括在无人机上测试我们提出的LIO-SAM系统。

七、参考文献

[1] J. Zhang 和 S. Singh，“低漂移实时激光雷达里程计与地图绘制”，《自主机器人》，第 41(2) 卷：401-416，2017 年。
[2] A. Geiger、P. Lenz 和 R. Urtasun，“我们准备好迎接自动驾驶了吗？KITTI 视觉基准套件”，IEEE 国际计算机视觉与模式识别会议，第 3354-3361 页，2012 年。
[3] P.J. Besl 和 N.D. McKay，“一种 3D 形状配准方法”，《IEEE 模式分析与机器智能学报》，第14(2): 239-256, 1992。
[4] A. Segal、D. Haehnel 和 S. Thrun，“广义 ICP”，《机器人学：科学与系统》论文集，2009 年。
[5] W.S. Grant、R.C. Voorhies 和 L. Itti，“在 LiDAR 点云中查找平面以实现实时配准”，IEEE/RSJ 智能机器人与系统国际会议，第 4347-4354 页，2013 年。
[6] M. Velas、M. Spanel 和 A. Herout，“利用领线段从 Velodyne 点云快速估计里程”，IEEE 机器人与自动化国际会议，第 4486-4495 页，2016 年。
[7] T. Shan 和 B. Englot，“LeGO-LOAM：轻量级且针对地面优化的可变地形激光雷达里程计和制图”，IEEE/RSJ 智能机器人与系统国际会议，第 4758-4765 页，2018 年。
[8] T. Shan、J. Wang、K. Doherty 和 B. Englot，“用于地形可穿越性测绘的贝叶斯广义核推理”，机器人学习会议，第 829-838 页，2018 年。
[9] S. Lynen、M.W. Achtelik、S. Weiss、M. Chli 和 R. Siegwart，“一种应用于微型飞行器导航的鲁棒模块化多传感器融合方法”，IEEE/RSJ 智能机器人与系统国际会议，第 3923-3929 页，2013 年。
[10] S. Yang、X. Zhu、X. Nian、L. Feng、X. Qu 和 T. Mal，“一种用于城市规模激光雷达测绘的鲁棒位姿图方法”，IEEE/RSJ 智能机器人与系统国际会议，第 1175-1182 页，2018 年。
[11] M. Demir 和K. Fujimura，“城市环境中低架多激光雷达的稳健定位”，IEEE智能交通系统会议，第3288-3293页，2019年。
[12] Y. Gao、S. Liu、M. Atia和A. Noureldin，“基于混合扫描匹配算法的城市和室内环境INS/GPS/激光雷达集成导航系统”，传感器，第15卷(9): 23286-23302，2015年。
[13] S. Hening、C.A. Ippolito、K.S. Krishnakumar、V. Stepanyan 和 M. Teodorescu，“城市 GPS 信号退化环境中无人机的 3D LiDAR SLAM 与 GPS/INS 集成”，AIAA Infotech@Aerospace会议，第 448-457 页，2017 年。
[14] C. Chen、H. Zhu、M. Li 和 S. You，“从基于滤波和基于优化的角度回顾视觉-惯性同步定位与地图构建”，Robotics，vol. 7(3):45, 2018。
[15] C. Le Gentil、T. Vidal-Calleja 和 S. Huang，“IN2LAMA：惯性激光雷达定位与建图”，IEEE 机器人与自动化国际会议，第 6388-6394 页，2019 年。
[16] C. Qin、H. Ye、C.E. Pranata、J. Han、S. Zhang 和 Ming Liu，“R-LINS：一种用于稳健高效导航的机器人中心激光雷达惯性状态估计器”，arXiv:1907.02233，2019 年。
[17] H. Ye、Y. Chen 和 M. Liu，“紧耦合 3D 激光雷达惯性里程计与建图”，IEEE 机器人与自动化国际会议，第 3144-3150 页， 2019。
[18] F. Dellaert 和 M. Kaess，“机器人感知的因子图”，《机器人学基础与趋势》，第 6 卷(1-2): 1-139，2017 年。
[19] M. Kaess、H. Johannsson、R. Roberts、V. Ila、J.J. Leonard 和 F. Dellaert，“iSAM2：使用贝叶斯树进行增量平滑和映射”，《国际机器人研究杂志》，第 31 卷(2): 216-235，2012 年。
[20] C. Forster、L. Carlone、F. Dellaert 和 D. Scaramuzza，“实时视觉惯性里程计的流形上预积分”，《IEEE 机器人学报》，第 6 卷(2): 216-235，2012 年。 33(1): 1-21, 2016。
[21] T. Moore 和 D. Stouch，“机器人操作系统的广义扩展卡尔曼滤波器实现”，智能自主系统，第 13 卷：335-348，2016。
[22] G. Kim 和 A. Kim，“扫描上下文：3D 点云地图中位置识别的自我中心空间描述符”，IEEE/RSJ 智能机器人与系统国际会议，第 4802-4809 页，2018。
[23] J. Guo、P. VK Borges、C. Park 和 A. Gawel，“使用激光雷达强度​​进行稳健位置识别的局部描述符”，IEEE 机器人与自动化快报，第 13 卷：335-348，2016。 4(2): 1470-1477, 2019。
[24] M. Quigley、K. Conley、B. Gerkey、J. Faust、T. Foote、J. Leibs、
R. Wheeler 和 A.Y. Ng，“ROS：一种开源机器人操作系统”，IEEE ICRA 开源软件研讨会，2009。
[25] T. Qin、P. Li 和 S. Shen，“Vins-mono：一种稳健且多功能的单目视觉惯性状态估计器”，IEEE 机器人学报，第 34(4): 1004-1020, 2018。

yan 25.8.30